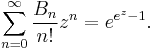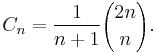Partition of a set

In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X. More formally, these "cells" are both collectively exhaustive and mutually exclusive with respect to the set being partitioned.

Contents

Definition

A partition of a set X is a set of nonempty subsets of X such that every element x in X is in exactly one of these subsets.

Equivalently, a set P is a partition of X if, and only if, it does not contain the empty set and:

  1. The union of the elements of P is equal to X. (The elements of P are said to cover X.)
  2. The intersection of any two distinct elements of P is empty. (We say the elements of P are pairwise disjoint.)

In mathematical notation, these two conditions can be represented as

1. \bigcup P = X
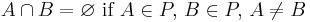
2. A \cap B = \varnothing \text{ if } A \in P,\, B\in P,\, A \neq B

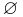where \varnothing is the empty set. The elements of P are called the blocks, parts or cells of the partition.[1]

Examples

Partitions and equivalence relations

For any equivalence relation on a set X, the set of its equivalence classes is a partition of X. Conversely, from any partition P of X, we can define an equivalence relation on X by setting x ~ y precisely when x and y are in the same part in P. Thus the notions of equivalence relation and partition are essentially equivalent.[2]

Refinement of partitions

Any partition α of a set X is a refinement of a partition ρ of X—and we say that α is finer than ρ and that ρ is coarser than α—if every element of α is a subset of some element of ρ. Informally, this means that α is a further fragmentation of ρ. In that case, it is written that α ≤ ρ.

This finer-than relation on the set of partitions of X is a partial order (so the notation "≤" is appropriate); it is a complete lattice. For the simple example of X = {1, 2, 3, 4}, the partition lattice has 15 elements and is depicted in the following Hasse diagram.

Another example illustrates the refining of partitions from the perspective of equivalence relations. If D is the set of cards in a standard 52-card deck, the same-color-as relation on D – which can be denoted ~C – has two equivalence classes: the sets {red cards} and {black cards}. The 2-part partition corresponding to ~C has a refinement that yields the same-suit-as relation ~S, which has the four equivalence classes {spades}, {diamonds}, {hearts}, and {clubs}.

Noncrossing partitions

A partition of the set N = {1, 2, ..., n} with corresponding equivalence relation ~ is noncrossing provided that there are no distinct numbers a, b, c, and d in N with a < b < c < d for which a ~ c and b ~ d. The lattice of noncrossing partitions of a finite set has recently taken on importance because of its role in free probability theory. These form a subset of the lattice of all partitions, but not a sublattice, since the join operations of the two lattices do not agree.

Counting partitions

The total number of partitions of an n-element set is the Bell number Bn. The first several Bell numbers are B0 = 1, B1 = 1, B2 = 2, B3 = 5, B4 = 15, B5 = 52, and B6 = 203. Bell numbers satisfy the recursion 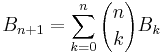B_{n%2B1}=\sum_{k=0}^n {n\choose k}B_k

and have the exponential generating function

\sum_{n=0}^\infty\frac{B_n}{n!}z^n=e^{e^z-1}.

The number of partitions of an n-element set into exactly k nonempty parts is the Stirling number of the second kind S(n, k).

The number of noncrossing partitions of an n-element set is the Catalan number Cn, given by

C_n={1 \over n%2B1}{2n \choose n}.

See also

Notes

  1. ^ Brualdi, pp. 44-45
  2. ^ Schechter, p. 54

References